Web Exclusive: Terminal Impact Force Analysis
Web Exclusive Sidebar to this month's "Safety Advice" column.
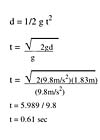The OSHA/ANSI minimum 5,000-pound (22.2kN) tensile strength requirement notwithstanding, we should investigate the formulas required to calculate the actual terminal impact forces imposed when a maximum allowable 310-pound (890N) mass free-falls 6 feet and is arrested. Keep in mind that there are only two sections of the subpart that declare a minimum tensile strength less than 5,000 pounds:
When we study fall force, we must consider it a vector quantity. That means that an applied force always has a vector (direction) and a magnitude (quantity) and displacement (distance):
F = force vector (typically based on X-Y-Z coordinates)
N = force magnitude in Newtons (1 Newton = 1 kilogram-meter per second2 ) 1000 Newtons = 1kN = 225 lbs
d = force displacement (in meters) 1 m = 3.2808 ft / 1 ft = 0.3048 m
Vt = terminal velocity of arrest fall distance = d / t
All forces, including the force of a falling body, can be measured by the effect of that force on a body's mass. The distance a body falls is also known as its force displacement value (d). If we were to fall in a straight, vertical direction, our vector quantity of force has both magnitude (meters) and direction. The displacement magnitude (d) of a 6-foot (arrested) fall would be denoted as:
d = 6 ft x 0.3048 m/ft = 1.83 m
Gravity is the force of attraction created by two or more bodies with unequal mass. The Earth's mass is 5.9 x 1024 kg while my mass is 90.6 kg. Falling vertically under the primary influence of earth's gravity (without any additional propulsion) causes my mass to increase in velocity the longer it continues to fall. Whenever the fall occurs outside of a pure vacuum, factors such as the minute centrifugal force or earth's rotation, wind resistance (friction), air temperature and relative humidity, surface area of the body presented to the fall vector, and even the type and configuration of clothing worn become critical. I have heard it estimated that depending on such factors, a 200-pound, 6-foot-tall falling man will accelerate to a terminal velocity of 165 mph (242 ft/sec or 73.76 m/sec) in a 213.4 m (700-foot) free fall . In this particular analysis, however, these limiting factors will not be considered. This expression in the change of velocity of a falling mass is called acceleration (a). Acceleration is also a vector quantity.
a = acceleration magnitude (meters per second per second - m/s2)
Newton's Second Law of Motion states that whenever any object with a mass (m) is acted upon by a force of magnitude (F), the magnitude of acceleration (a) or deceleration (-a) may be calculated using the formula:
a = F/m (acceleration = Force/mass)
For example, when a 200-pound (90.6 kg) worker falls, he accelerates downward toward the surface of the earth at 32 ft/sec2 (9.75m/sec2), which is the average acceleration magnitude (aavg) of gravity at earth's surface of 1 g. Consider he free falls a distance (d) of 6 feet (1.828m) before being arrested to a stop without a deceleration device. We must calculate the Terminal Impact Force (TIF) that would be applied to this body at the instant of his arrested fall.
One of the values that could be calculated is the time (t) it takes a 200-pound (90.6 kg) mass to fall 6 feet (d=1.82 m) at one earth (g) of 9.8m/s2. The original force displacement (distance) formula will apply as shown in Figure 1:
Therefore, it takes about 0.6 seconds for the worker to free-fall 6 ft (1.83 m)
So the terminal velocity of the mass after arresting a fall at 6 feet is 5.99 m/s (19.65 ft/sec), which is equivalent to hitting a brick wall at almost 14 mph in your car while wearing your seat belt. We can check this value because we already calculated the total fall time as 0.61 seconds. If the average acceleration rate is 9.8 m/sec2, then we can also check the terminal velocity based on time rather than distance:
Vt = aavg x t
Vt = (9.8m/s2) x (0.61s)
Vt = 5.98 m/s
According to the skydivers I have spoken with, the average, "real life" terminal velocity of the falling 200-pound man is approximately 145 mph (64.8 m/sec). According to the fall time formula, it would take 6.6 seconds to reach this speed Reformulating the velocity formula, the total free-fall distance required to reach this velocity is over 214 meters (700 feet).
a= Vt2 / (2)Sd
a = (-5.98 m/s)2 / 2 (0.152 m)
a= (-35.76 m/s2) / (0.304m)
a= -117.63 m/s2
Md = -a / (9.8)g
Md = (-117.63 m/s2) / (9.8 m/s2)g
Md = -12.00 g
Fi = W x Md
Fi = 200 lbs x (-12.00)g
Fi = -2,400 lbs (10.66 kN)
While this terminal impact force is an accurate calculation under laboratory precise conditions, our TIF is safety factored by 2X to produce a maximum rated load of 4,800 pounds (21.3 3kN) under "real-life" site conditions. This is less than less than the 5,000-pound (22.2 kN) tensile strength required by OSHA (1926.502(d)(15) per attached worker by a factor of -0.04. Each and every component of a personal fall arrest system designed for 5,000 pounds minimum tensile strength, including the terminal anchor point, would be capable of resisting this force without failure by a factor of 2.04.
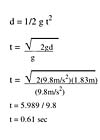
Figure 1.
- 1926.502(d)(4) states that the D-rings and snap hooks in the system be proof-tested to 3600 (16kN) tensile strength "without cracking, breaking or taking permanent deformation."
- 1926.502(d) states that whenever self-retracting lifelines/lanyards automatically limit free fall distance to 2 feet or less, "they shall be capable of sustain a minimum tensile load of 3,000 pounds (13.3kN)."
When we study fall force, we must consider it a vector quantity. That means that an applied force always has a vector (direction) and a magnitude (quantity) and displacement (distance):
F = force vector (typically based on X-Y-Z coordinates)
N = force magnitude in Newtons (1 Newton = 1 kilogram-meter per second2 ) 1000 Newtons = 1kN = 225 lbs
d = force displacement (in meters) 1 m = 3.2808 ft / 1 ft = 0.3048 m
Vt = terminal velocity of arrest fall distance = d / t
All forces, including the force of a falling body, can be measured by the effect of that force on a body's mass. The distance a body falls is also known as its force displacement value (d). If we were to fall in a straight, vertical direction, our vector quantity of force has both magnitude (meters) and direction. The displacement magnitude (d) of a 6-foot (arrested) fall would be denoted as:
d = 6 ft x 0.3048 m/ft = 1.83 m
Gravity is the force of attraction created by two or more bodies with unequal mass. The Earth's mass is 5.9 x 1024 kg while my mass is 90.6 kg. Falling vertically under the primary influence of earth's gravity (without any additional propulsion) causes my mass to increase in velocity the longer it continues to fall. Whenever the fall occurs outside of a pure vacuum, factors such as the minute centrifugal force or earth's rotation, wind resistance (friction), air temperature and relative humidity, surface area of the body presented to the fall vector, and even the type and configuration of clothing worn become critical. I have heard it estimated that depending on such factors, a 200-pound, 6-foot-tall falling man will accelerate to a terminal velocity of 165 mph (242 ft/sec or 73.76 m/sec) in a 213.4 m (700-foot) free fall . In this particular analysis, however, these limiting factors will not be considered. This expression in the change of velocity of a falling mass is called acceleration (a). Acceleration is also a vector quantity.
a = acceleration magnitude (meters per second per second - m/s2)
Newton's Second Law of Motion states that whenever any object with a mass (m) is acted upon by a force of magnitude (F), the magnitude of acceleration (a) or deceleration (-a) may be calculated using the formula:
a = F/m (acceleration = Force/mass)
For example, when a 200-pound (90.6 kg) worker falls, he accelerates downward toward the surface of the earth at 32 ft/sec2 (9.75m/sec2), which is the average acceleration magnitude (aavg) of gravity at earth's surface of 1 g. Consider he free falls a distance (d) of 6 feet (1.828m) before being arrested to a stop without a deceleration device. We must calculate the Terminal Impact Force (TIF) that would be applied to this body at the instant of his arrested fall.
One of the values that could be calculated is the time (t) it takes a 200-pound (90.6 kg) mass to fall 6 feet (d=1.82 m) at one earth (g) of 9.8m/s2. The original force displacement (distance) formula will apply as shown in Figure 1:
Therefore, it takes about 0.6 seconds for the worker to free-fall 6 ft (1.83 m)
Figure 2.
Step 1
In order to begin to determine the impact force of a mass falling 6 feet, the instantaneous velocity of the mass must first be determined. The instantaneous (or terminal) velocity (Vt) which the mass achieves in a 6-foot (1.83 m) free fall may be calculated by using either a time or distance qualified formula. The distance formula follows in Figure 2:So the terminal velocity of the mass after arresting a fall at 6 feet is 5.99 m/s (19.65 ft/sec), which is equivalent to hitting a brick wall at almost 14 mph in your car while wearing your seat belt. We can check this value because we already calculated the total fall time as 0.61 seconds. If the average acceleration rate is 9.8 m/sec2, then we can also check the terminal velocity based on time rather than distance:
Vt = aavg x t
Vt = (9.8m/s2) x (0.61s)
Vt = 5.98 m/s
According to the skydivers I have spoken with, the average, "real life" terminal velocity of the falling 200-pound man is approximately 145 mph (64.8 m/sec). According to the fall time formula, it would take 6.6 seconds to reach this speed Reformulating the velocity formula, the total free-fall distance required to reach this velocity is over 214 meters (700 feet).
Step 2
Next, the total deceleration (negative acceleration) force (a) at terminal impact will be calculated. A total deceleration distance (Sd) of merely 6 inches (0.152m) is chosen, allowing for the initial elongation of the nylon straps of the lanyard and harness and the compression of body tissues. Deceleration force (a) can be calculated by the following equation:a= Vt2 / (2)Sd
a = (-5.98 m/s)2 / 2 (0.152 m)
a= (-35.76 m/s2) / (0.304m)
a= -117.63 m/s2
Step 3
Next, solve for a deceleration multiplier (Md) of the force of gravity (g), where (a) equals the previously calculated deceleration force. We can calculate by the following:Md = -a / (9.8)g
Md = (-117.63 m/s2) / (9.8 m/s2)g
Md = -12.00 g
Step 4
Finally, we calculate the terminal impact force (Ft) by multiplying the deceleration multiplier (Md) times the mass (W) of the falling victim. We agreed for this problem that at 1 g, mass (in kilograms) and weight (in pounds) are equal. As the deceleration multiplier (Md) figure is without scalar units, we can calculate (Ft) in either pounds or kilograms. In this case the falling victim initially weighed 200 lbs (90.6 kg). The following formula determines how many pounds of deceleration (impact) force (Ft) would be applied to his body after a 6foot (1.83 m) free-fall termination with only a 6-inch deceleration distance:Fi = W x Md
Fi = 200 lbs x (-12.00)g
Fi = -2,400 lbs (10.66 kN)
While this terminal impact force is an accurate calculation under laboratory precise conditions, our TIF is safety factored by 2X to produce a maximum rated load of 4,800 pounds (21.3 3kN) under "real-life" site conditions. This is less than less than the 5,000-pound (22.2 kN) tensile strength required by OSHA (1926.502(d)(15) per attached worker by a factor of -0.04. Each and every component of a personal fall arrest system designed for 5,000 pounds minimum tensile strength, including the terminal anchor point, would be capable of resisting this force without failure by a factor of 2.04.
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!
